[视频]参数方程的二阶导数的计算方法

来自搜狐视频https://tv.sohu.com/的优秀用户互联网实用攻略，于2020-05-16在生活百科知识平台总结分享了一篇关于“参数方程的二阶导数的计算方法东风标致308s”的经验，非常感谢互联网实用攻略的辛苦付出，他总结的解决技巧方法及常用办法如下：

很多人在参数方程的导数计算方式上容易出错，有些人可能一时间看着书本或者答案也还是有点糊涂，主要是因为参数多了。小编这里分别以公式和例题来做个讲解，希望能对大家有所帮助。

一、先来看下公式

1/3分步阅读

已知有x和y都是关于t的参数方程，求y对x的二阶导数

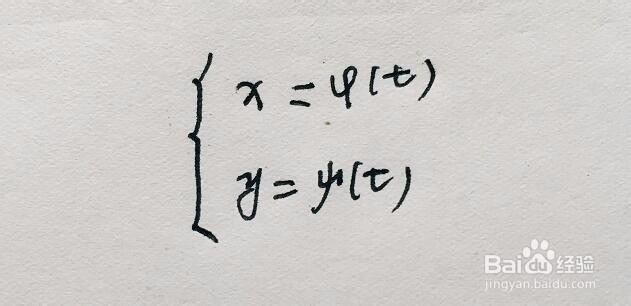[图]2/3

我们先来求一阶导数：

dy/dx=dy/dt *dt/dx= dy/dt / dx/dt, 所以y对x的一阶导数就等于y对t的一阶导数除以x对t的一阶导数

说明：因为，y和x都是关于t的参数方程，所以求dy/dx时，需要中间增加了dt作为桥梁，使得y和x对t求导。

[图]3/3

再来求二阶导数：把对x求导转化为对t求导

二阶求导就是把上个步骤我们求出来的一阶导数再次求导，但要记住是对x参数求导，而一阶导数实际上仍然是关于t的方程。所以需要和求一阶导数过程一样的，再次增加dt为桥梁，就变成了一阶导数对t求导再除以x对t求导。如图看过程，主要是红框中增加dt为桥梁的转换，后面就是正常的求导了。

[图]

二、举例子说明

1/5

有如图所示的参数方程

x和y都是关于t的参数方程，求y对x的二阶导数

[图]2/5

我们先求一阶导数：

一阶导数还是比较容易的，根据上述关于公式的说明中，已经提到，x和y是关于t的参数，所以不能直接求dy/dx，而是增加了dt 来作变换后分别进行y和x对t的求导。

[图]3/5

上述求导中，将结果进行化解，利用三角函数的一些公式，可以化解得到结果

所以一阶导数就等于cot（t/2）

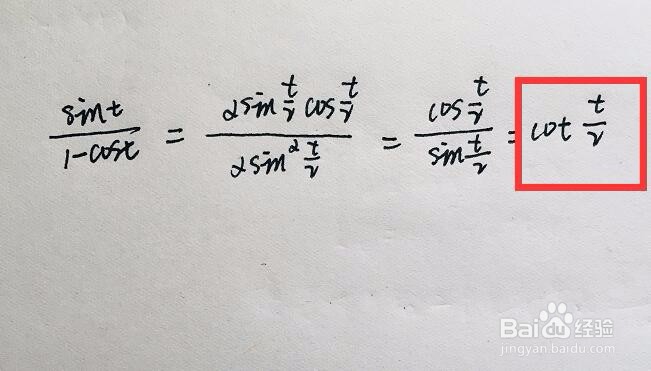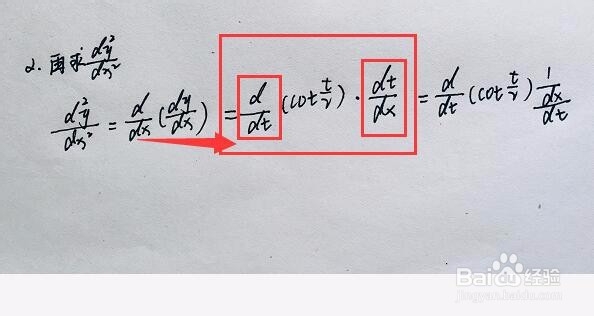
[图]4/5

将一阶导数再次求导，牢记分辨参数，这里依然是对x进行再次求导。

而一阶导数cot（t/2）是个关于t的参数，不能对x直接求导，所以继续增加dt为桥梁变换为对t进行求导。

这一步最为关键，很多人会直接把一阶导数cot（t/2） 直接对t求导，就出错了。

[图]5/5

再往下就简单了，都是对t的正常求导了。

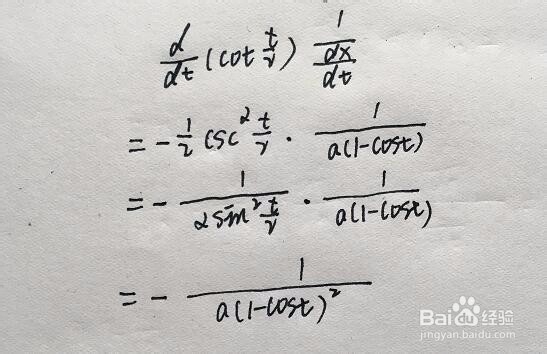[图]参数方程二阶导数计算方法

编辑于2020-05-16，内容仅供参考并受版权保护